LINE LOSS CALCULATION: SAMPLE PROBLEM 1

PROBLEM: A 3-kilometer, 336ACSR, 3-wire short transmission line has an impedance of 2 + j5 ohms per wire. At the receiving end, a balanced 3-phase load and capacitor bank draws 3000kVA, 0.71 power factor lagging and 600kVAR respectively at 8000 volts per phase to neutral. Determine the power loss of the transmission line.

SOLUTION:

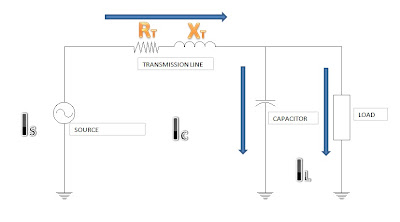
The first thing that we should do in analyzing any problem is to illustrate our interpretation of the problem into a figure which will make us better understand what is needed.

In this problem, we are asked to compute for the transmission line loss with the following given data:

Transmission line impedance of 2 + j5
3-phase load of 3000kVA at 71% power factor lagging.
Capacitor of 600kVAR
8000 volts per phase to neutral.

To see various conductor resistance for ACSR wires, you can refer to RESISTANCE TABLE

Basing upon the above diagram, we now compute for the current that passes through the capacitor and the load using the formula below.

IL = KVAL / (3 x Voltage L) = 3,000,000 /(3x8000) = 125A

θL = arccos(0.71) = 44.765 degrees

IC = kVARC /(3 xVoltage C) = 600,000 / (3x8000) = 25A

The next step is to calculate for the current that passes through the transmission line by adding the load current and the capacitor current vectorially.

IT = IC + IL

= 25 angle 90 degrees + 125 angle (-44.765 degrees)

= j25 +88.75 - j88.025

IT = 88.75 - j63.025 = 108.85 angle (-35.38 degrees)

The final part of this solution is to compute for the total line losses in the three lines by using the power loss formula.

As a result, the total transmission line loss would be.

PLoss = 3 (108.85)2(2)

PLoss = 71.09 kilowatts

Reference: 1001 Solved Problems in Electrical Engineering by Romeo Rojas Jr.

Comments

PARTS OF A POWER TRANSFORMER

What are the name of the basic parts of a Power Transformer? We can not deny the fact that only a handful of electrical engineering students are presently familiar with power transformers especially on what it looks like. Unlike a transformer we found in our homes, a power transformer’s appearance and construction is somewhat more complicated. It is not just a simple winding with a primary and secondary terminal although basically any transformer has one. The function that a power transformer plays in an electrical system is very important that an electric utility can not afford to loss it during its operation. Our discussion here will focus more on the basic parts and functions of a power transformer that are usually tangible whenever you go to a substation . Although not all power transformers are identical, nonetheless they all have the following listed parts in which the way of construction may differ.

click here to continue

ELECTRIC MOTOR NAMEPLATE SPECIFICATIONS

How do we interpret an electric motor nameplate? Motor standards are established on a country by country basis.Fortunately though, the standards can be grouped into two major categories: NEMA and IEC (and its derivatives). In North America, the National Electric Manufacturers Association (NEMA) sets motor standards, including what should go on the nameplate (NEMA Standard MG 1-10.40 "Nameplate Marking for Medium Single-Phase and Polyphase Induction Motors").

click here to continue

DISADVANTAGES OF Y-Y CONNECTION IN THREE PHASE SYSTEM

What are the disadvantages in using y-y connection? The Y-Y transformer connection was poorly understood in the early days of power engineering and it received a very bad reputation when it was first used; in fact, this connection was avoided for a long time until its limitations were overcome by good engineering practice. Some of the inherent disadvantages of the Y-Y connection are discussed below:

click here to continue

power systems loss

Search This Blog